넓이 문제
직선을 변으로 갖는 영역들에 대해서 넓이라는 단어는 생각하기 쉽다. 그러나 곡선으로 된 영역의 넓이를 구하는 것은 그렇게 쉽지 않다.
접선을 정의할 때 먼저 접선의 기울기를 할선들의 기울기에 대한 극한으로 근사시켰음을 상기, 넓이에 대해서도 이와 비슷한 아이디어를 따른다. 영역 S 를 직사각형들로 근사시킨 다음에 이 직사각형들의 수를 증가시켜서 직사각형들의 넓이의 극한을 구한다.
예제
0부터 1 까지 포물선 y = x^2 아래의 넓이를 직사각형들을 이용하여 구한다.
먼저 영역 S 는 한 변의 길이가 1인 정사각형 안에 포함되기 때문에 S 의 넓이는 0과 1 사이의 어떤 값임을 알 수 있다. 좀 더 정확한 값을 구하기 위해 각 구간을 나눌 수 있다.
각 조각들을 직사각형으로 근사시킬 수 있다. 직사각형의 높이들은 오른쪽 끝 점에서 함수 f(x) = x^2 의 값들이다.
또는 왼쪽 끝 점에서 함수 f 의 좀 더 작은 직사각형을 이용할 수도 있다.
우리가 원하는 넓이에 대한 상한, 하한의 측정값을 갖게 된다.
왼쪽 끝 < S < 오른쪽 끝
조각들의 숫자를 더 많게 하면서 좀 더 정확한 하한, 상한 근삿값을 얻을 수 있다.
정의
연속함수 f 의 그래프 아래에 놓여 있는 영역 S 의 넓이 A 는 직사각형들의 넓이의 합에 대한 극한이다.
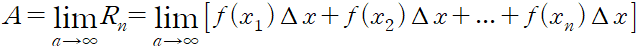
위의 극한은 함수 f 가 연속이라고 가정했기 때문에 항상 존재함을 증명할 수 있다. 또한 부분 구간들의 왼쪽, 오른쪽 끝 점들을 사용한 경우에도 동일한 값을 얻을 수 있다.
거리 문제
거리 문제를 생각, 물체의 속도가 알려졌을 경우 어떤 시간 동안 그 물체가 이동한 거리를 구한다.
물체의 속도가 일정하다면
거리 = 속도 * 시간
공식에 의해 쉽게 풀린다. 그러나 속도가 변한다면 이동한 거리를 계산하는 것은 쉽지 않다.
이 또한 넓이를 측정하기 위해서 사용했던 합을 사용하여 해결할 수 있다.
'미적분 > 미분적분학' 카테고리의 다른 글
| 5.3 미적분학의 기본 정리 (1) | 2022.12.25 |
|---|---|
| 5.2 정적분 (0) | 2022.12.25 |
| 4.3 그래프의 모양을 말해주는 도함수 (2) | 2022.12.24 |
| 4.2 평균값 정리 (0) | 2022.12.24 |
| 4.1 최댓값과 최솟값 (0) | 2022.12.24 |



