미분적분학의 많은 응용은 함수 f 에 대한 여러 사실들을 도함수에 관한 정보로부터 유추하는 능력에 달려 있다.
f'(x) 는 점 (x, f(x)) 에서 곡선 y=f(x) 의 기울기를 표현하기 때문에 곡선이 각각의 점에서 진행하는 방향을 알려준다.
따라서 f'(x) 가 f(x) 에 대한 정보를 제공하리라고 기대하는 것은 무리가 아니다.
f' 은 f 에 대해 무엇을 알려주는가?
f 의 미분이 함수가 어디에서 증가 또는 감소인지를 알 수 있다.
f'(x) 가 양수일 때 f 는 증가이고 f'(x) 가 음수일 때 f 는 감소이다. 이것이 항상 성립함을 보이기 위해 평균값 정리를 이용한다.
증가감소 판정법
- 어떤 구간에서 f'(x) > 0 이면, f 는 증가이다.
- 어떤 구간에서 f'(x) < 0 이면, f 는 감소이다.
증가감소 판정법을 이용하기 위해 어디에서 f'(x) > 0 이고, 어디에서 f'(x) < 0 인지를 알아야 한다. 이 부등식을 풀기 위해 f'(x)=0 의 근을 구한다.
이 값들이 f 의 임계수이고 정의역을 각 구간으로 나눈다. 각 구간에서 f'(x) 는 항상 양수이거나 항상 음수이다. 이 중 어디에 해당하는지는 f'(x) 의 인수의 부호를 따져보면된다.
극값
f 가 c 에서 극대나 극소를 갖는다면 c 는 f 의 임계수이어야만 하나, 모든 임계수가 최대나 최소를 나타내는 것은 아님을 기억할 것이다. 그러므로 f 가 임계수에서 극대나 극소를 갖는지 여부를 알 수 있는 판정법이 필요하다.
f'(x) 의 부호가 바뀌는 부분으로부터 다음 판정법을 만들 수 있다.
일계도함수 판정법
c 가 연속함수 f 의 임계수라고 하자.
- 만일 f' 이 c 에서 양수에서 음수로 변한다면, f 는 c 에서 극댓값을 갖는다.
- 만일 f' 이 c 에서 음수에서 양수로 변한다면, f 는 c 에서 극솟값을 갖는다.
- 만일 f' 이 c 에서 부호가 변하지 않는다면 f 는 c 에서 극대나 극소를 가지지 않는다.
일계도함수 판정법은 증가감소 판정법에 따른 것이다.
f'' 은 f 에 대해 무엇을 말하는가?
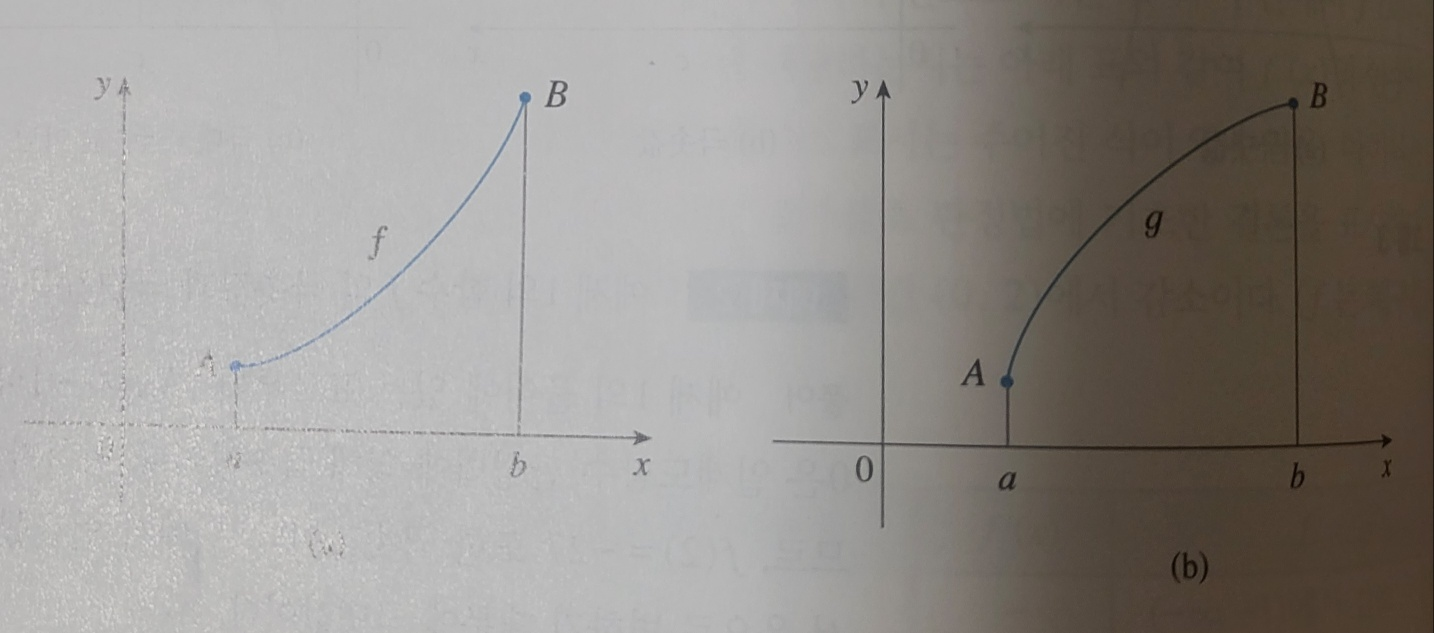
두 개의 증가함수 그래프, 이들 그래프는 점 A 와 점 B 를 연결하지만 다른 방향으로 굽어 있으므로 다르게 보인다.
a 에서의 곡선은 접선 위에 있는데 이때 f 를 (a,b) 에서 위로 오목이라고 부른다. b 에서의 곡선은 접선 아래에 있는데 아래로 오목이라고 부른다.
정의
f 의 그래프가 구간 I 에서 함수의 모든 접선 위에 존재한다면 이것은 I 에서 위로 오목이라고 부른다. f 의 그래프가 구간 I 에서 함수의 모든 접선 아래에 존재한다면 이것은 I 에서 아래로 오목이라고 부른다.
오목성 판정법
- I 의 모든 x 에 대하여 f''(x) > 0 이라면, f 의 그래프는 I 에서 위로 오목하다.
- I 의 모든 x 에 대하여 f''(x) < 0 이라면, f 의 그래프는 I 에서 아래로 오목하다.
정의
곡선 f 가 점 P 에서 연속이고 곡선이 그곳에서 위로 오목에서 아래로 오목으로 또는 아래로 오목에서 위로 오목으로 변한다면, 그 곡선 위의 점 P 를 변곡점 inflection point 라고 부른다.
이계도 함수의 다른 응용은 극대와 극소에 대한 다음의 판정법이다.
이계도함수 판정법
f'' 이 c 근방에서 연속이라고 하자
- f'(c) = 0 이고 f''(c) > 0 라면, f 는 c 에서 극소를 갖는다.
- f'(c) = 0 이고 f''(c) < 0 라면, f 는 c 에서 극대를 갖는다.
'미적분 > 미분적분학' 카테고리의 다른 글
| 5.2 정적분 (0) | 2022.12.25 |
|---|---|
| 5.1 넓이와 거리 (1) | 2022.12.25 |
| 4.2 평균값 정리 (0) | 2022.12.24 |
| 4.1 최댓값과 최솟값 (0) | 2022.12.24 |
| 3.11 쌍곡선함수 (0) | 2022.12.24 |


