1.3.4 양자회로

양자회로의 요소에 대해 자세히 살펴본다. 그림은 3개의 양자 게이트가 포함된 간단한 양자회로이다. 

회로는 왼쪽에서 오른쪽으로 읽어야 한다. 회로의 각 선은 양자회로의 도선을 나타낸다. 이 도선은 반드시 물리적인 도선에 해당하는 것은 아닌것으로, 시간 경과를 대신에서 나타낼 수 있고 공간을 통해 한 위치에서 다른 위치로 이동하는, 광자와 같은 물리적 입자를 의미할 수도 있다. 

회로에 대한 상태 입력이 계산기저 상태라고 가정하는 것이 일반적인데 보통 모두 |0> 으로 구성된 상태를 말한다. 

그림의 회로는 간단하지만 유용한 일을 한다. 즉, 두 큐비트의 상태를 서로 바꾼다. 이 회로가 어떻게 스왑 연산 swap epperation 을 하는지 알려면 한 무리의 게이트가 계산기저 상태인 |a, b> 에서 일련의 효과

를 일으키는 것에 주목하면 된다. 여기서 모든 덧셈은 모듈러 2 에관해 수행된다. 그러므로 이 회로는 두 큐비트의 상태를서로 바꾸는 효과를 낸다.

양자회로에는 일반적으로 존재하지 않지만 고전회로에서 허용되는 기능들이 있다. 먼저, 양자회로에서는 한 부분에서 다른 부분으로 피드백하는 루프를 허용하지 않는다. 

이것을 회로가 비순환적 acyclic 이다라고 말한다. 둘째, 고전회로에서는 도선들을 하나로 모을 수 있는데 이 연산을 팬인 FANIN 이라고 하며 그 결과로 입력들을 비트별 bitwise OR 하여 단일 도선으로 만들 수 있다. 당연히 이 연산은 비가역적, 유니타리가 아니므로 양자회로에서는 팬인을 허용하지 않는다. 

셋째, 비트의 여러 복사본을 생성하는 역연산 inverse operation, 즉 팬아웃 FANOUT 도 양자회로에서는 허용되지 않는다. 사실, 양자역학은 큐비트의 복사를 금ㄱ지해 팬아웃 연산을 불간으하게 만드는 것으로 밝혀졌다.

필요할 때마다 새로운 양자 게이트의 도입, 양자회로에 대한 규칙들을 알아 놓는다. 

U 가 어떤 수 n 개의 큐비트들에 작용하는 유니타리 행렬이라고 가정하면, U 를 그 큐비트들에 대한 양자 게이트로 간주할 수 있다. 그러면 제어형 NOT 게이트를 자연스레 확장시킨 제어형 U 게이트 controlled-U gate 를 정의할 수 있다. 이 게이트는 검은 점이 있는 선으로 표시한 단일 제어 큐비트 control qubit 와 사각형 U 로 표시한 n 개의 대상 큐비트 n target qubits 를 포함한다. 제어 큐비트를 0으로 설정하면 대상 큐비트에는 아무런 변화가 없다. 제어 큐비트를 1로 설정하면 게이트 U 가 대상 큐비트에 적용된다. 제어형 U 게이트의 원형 예는 제어형 NOT 게이트인데 그림에 나타낸 것과 같이 U = X 가 되는 제어형 U 게이트이기도 하다.

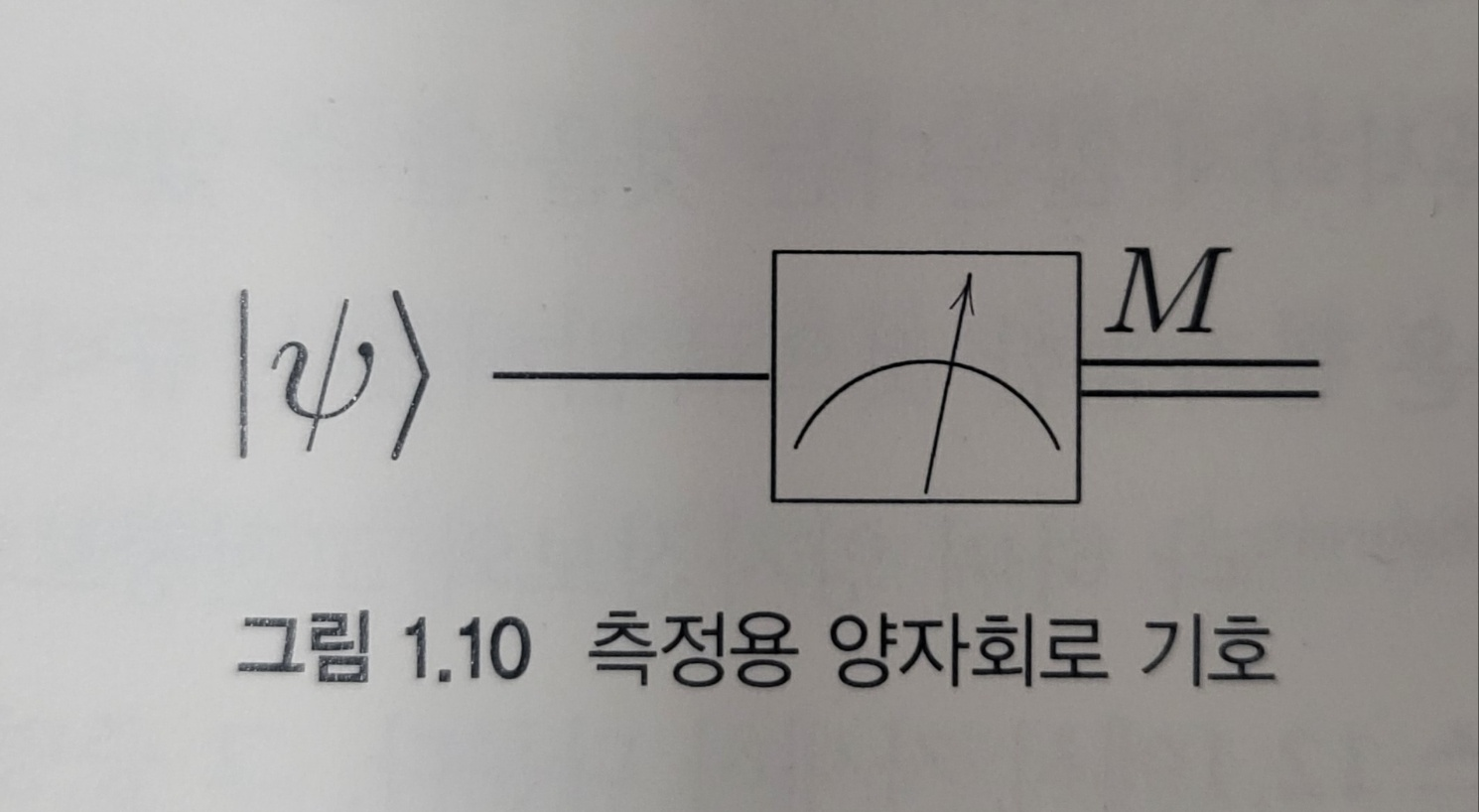
또 다른 중요한 연산은 측정이며 그림과 같이 미터기 기호로 나타낸다. 이 연산은 단일 큐비트 상태를 확률적인 고전비트 M 으로 변환한느데, 이때 0이 나올 확률은 |a|^2 이고 1이 나올 확률은 |b|^2 이다.

양자회로는 계산, 통신 및 양자 노이즈를 포함한 다양한 양자 프로세스를 구현하는 데 유용하다.